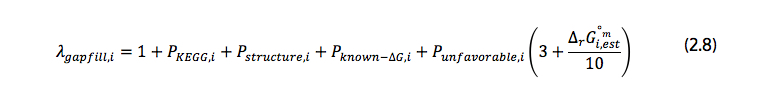This App allows a user to identify the minimal set of biochemical reactions missing in a draft metabolic model. It then fills in missing reactions in the model based on media stoichiometry to enable the modeled organism to produce biomass in a specified media.

Draft metabolic models usually have missing reactions due to incomplete or incorrect functional genome annotations. As a result, these models are unable to generate biomass on media where the organism typically is capable of growing. Gapfilling algorithms can be used to overcome this problem. These algorithms tentatively bridge gaps in metabolic pathways by identifying the minimal number of biochemical reactions to add to the draft metabolic model, thereby enabling it to produce biomass in a specified media. Note that gapfilled reactions are assertions based on annotations missed by the standard annotation pipeline, including the missed genes that encode these functions.

Starting with a draft metabolic model, imported or generated by the Build Metabolic Model App, we can apply the Gapfill Metabolic Model App to identify and fill all the gaps in the metabolic pathways of our models that might prevent the production of biomass for the organism or community. This is achieved by one of two ways: (i) relaxing reversibility constraints on the model s reactions or (ii) adding new reactions to the existing model. In this gapfilling process, the model is augmented to include all (i.e., about 13,000) biochemical reactions contained in the ModelSEED [1] database (available for download from GitHub). The database consists of reactions from KEGG, MetaCyc, EcoCyc, plant BioCyc, Plant Metabolic Networks, and Gramene.

During the gapfilling process, all reactions determined to be thermodynamically reversible [2-4] are adjusted to be reversible in the gapfilled metabolic model. Finally, flux balance analysis (FBA) [5] is performed to generate a flux profile that prioritizes the production of biomass while minimizing the flux through all reactions and reaction directions that were added in the gapfilling process. This method is consistent with previously published algorithms for gapfilling reaction networks [6,7]. All reactions and reaction directions generated by these algorithms that were not included in the drat model and have a nonzero flux are them added to the gapfilled model. This gapfilling solution subsequently permits growth of the metabolic model in the specified media condition. To see the reactions and reaction directions added by the gapfilling process, click the Reactions tab in the output table, and sort it by the Gapfilling column title.

The detailed 2-step gapfilling algorithm is illustrated in the first image at the top of this detail page (see above) and described below.

The objective function (2.1 and 2.4) minimizes the number of reactions, which are not present in the model but should be added for biomass to be produced in those conditions. Since, in this case, there is a false negative prediction, at least one reaction will need to be added.

In the formulation, all reactions are treated as reversible, with every reversible reaction being decomposed into two reactions in each direction, one in the forward direction and the other in the backward direction. This allows for the independent addition of each direction in the algorithm. As a result of this, reactions represented in the formulation are the forward and backward components of the reactions in the database. In the objective function, r_gapfilling represents the total number of reactions in the database; in objective function (2.1), v_i is the flux through reaction i; in objective function (2.4) Z_i is a binary variable equal to zero if the flux through reaction i is zero and one otherwise; and, λ_gapfill,i is a constant value stating the energy cost associated of adding reaction to the model. If reaction i is already present in the model, λ_gapfill,i is zero. Otherwise, λ_gapfill,i is calculated using equation (2.8). This equation is illustrated in the second image at the top of this detail page (see above) and described below.

Each of the P variables in equation (2.8) is binary, representing a penalty applied when adding different types of reactions to the model: they are equal to one if the penalty applies to the type of the particular reaction and equal to zero otherwise.

• P_KEGG,i is related to reactions not in KEGG.
• P_structure,i to the addition of reactions involving metabolites with unknown structure.
• P_known-ΔG,i to reactions for which cannot be calculated.
• P_{unfavorable,i} to reactions operating in an unfavorable direction.

Equation (2.2 and 2.5) implements the mass balance constraints related to the steady-state assumption of FBA. Here, N_reactionDB is the stoichiometric matrix, and v flux vector through reaction database.

Equation (2.6) enforces the bounds on reaction fluxes (v_i), and the values of the reaction use variables (Z_i). This equation ensures that each reaction flux, v_i, is zero unless Z_i is one. The v_max,i term in equation (2.6) is the core to the simulation using FBA. If v_max,i corresponds to a reaction associated with a knocked-out gene, v_max,i is set to zero. If v_max,i corresponds to the uptake of a nutrient not in the medium, v_max,i is also set to zero.

Equation (2.3 and 2.7) constrains the biomass flux, v_bio, to a nonzero value, to ensure growth.

The result of the gapfilling optimization includes a list of irreversible reactions from the model that should be made reversible and a set of reactions not in the model that should be added to fix a false negative prediction.

This App has been created as part of a suite of tools and data that support the reconstruction, prediction, and design of metabolic networks in KBase. For more help with metabolic modeling, please view the Metabolic Modeling FAQ.

Team members who developed & deployed algorithm in KBase: Chris Henry, Janaka Edirisinghe, Sam Seaver, and Neal Conrad. For questions please contact us.